Evrenimizin şekli düz geometriye sahiptir. Düz geometri, bir çizgi çizdiğimizde onun eğri değil, düz olmasıdır. Yapılan hesaplamalar evrenimizin 3 şekle sahip olabileceğini gösterir: küre, eyer ve düz. Alan-madde miktarına göre evrenimiz düz bir geometriye sahiptir. Şimdi bunun detaylarına maddeler hâlinde bakalım.
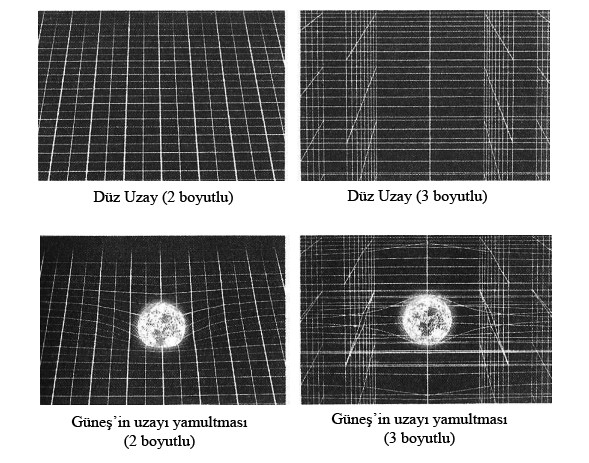
Brian Greene, “Evrenin Dokusu…”, age., s. 86, 87. (bk. Figür Kaynakları, Figür 33)
Kütle çekimi evreni büker (yamultur, eğriltir; uzatır, büzüştürür) ve evrenin her yerinde az-çok vardır, bu yüzden evrenin her tarafı eğri büğrüdür.
Madde (enerji) olmasaydı evren (uzay-zaman) düz olurdu, ama madde olmasaydı da evren olmazdı.
Kütle çekimi vesaireyi ihmal edersek aynı hızda, aynı yönde ilerleyen bir cisim, düz bir doğruda gider. Ama hızı sürekli değişen (ivmelenen) bir cisme göre -aynı yönde gittiğini sansa bile- evren eğilir (yamulur).
3 boyut en, boy, genişlikten, 2 boyut en ve boydan oluşur, yani 2 boyutun kalınlığı olmadığından ona tam olarak yandan bakarsak onu göremeyiz ama biraz açı yapıp ona bakarsak onu görmeye başlarız. Bir küre düşünün bunun yüzeyi 2 boyutlu olsun ya da küçükten büyüğe iç içe geçen içi boş 2 boyutlu küre yüzeyleri bir küreyi oluştursun. Bu yüzeylerden biri -3 boyutlu- kürenin bir parçasıdır. Şimdi de bir kitap düşünün, herhangi bir sayfasına 2 boyutlu diyelim. Bu sayfa da kitabın bir parçasıdır. Şimdi de -3 boyutlu- lastik bir küp düşünün, bundan da sayfa gibi 2 boyutlu bir kesit alırsak bu da bu küpün bir parçasıdır. Şimdi ise zamana 4. boyut diyelim. Bu 3 boyutlu örneklerin 4. boyut olan zamanın bir parçası olduğunu düşünelim. İşte bu şekli zihinde canlandıramıyoruz, bu yüzden evrenimizin şekli işte tam olarak budur diyemiyoruz, yani “var” ama diyemiyoruz değil, evren, “şekil” durumuna, şekle, biçime, görüntüye uymuyor, yani evren “şekil”den öte bir durum. Bu yüzden evrenin ucuna gelirsek ne olur, diye bir soru yanlış, evrenin ucu yok. Biz 3 boyutlu düşündüğümüz için, evren sonlu mu, sonundan sonra ne var, ondan sonra ne var, gibi sorular soruyoruz, ama 4. boyutta bu sorular geçersiz.
Evrenimizin kenarı, sınırı yoktur.
Zamanı eklemeden evrenimiz sonlu (sınırlı hacim), sınırsızdır (kenarı yok). 3 boyutlu düşündüğümüzde evrenin ucunda Big Bang ile o oluşmuş ilk ışıklar ışık hızında ilerlemektedir, varabileceğimiz son yer burasıdır, ama burada ışık olmamız lazım, ışık olursak -ışıkta zaman kavramı olmadığı için- zaman geçersizdir, burayı düşünemeyiz, ama bunun bir önceki evren kısmını düşünebiliriz, burada ilerlersek sonsuza kadar yeni yollarda yürürüz. 4 boyutlu düşünseydik eğer -ki bu nasıl olur, bilinmiyor- ve o ilk ışıkları da düşüncemize ekleseydik evrenin şekli için sınırlı ya da sınırsız, -burası önemli- sonlu ya da sonsuz kavramları bile düşerdi, geçersiz olurdu. Evrenimiz sadece 3 boyutta sonlu ve sınırsızdır.
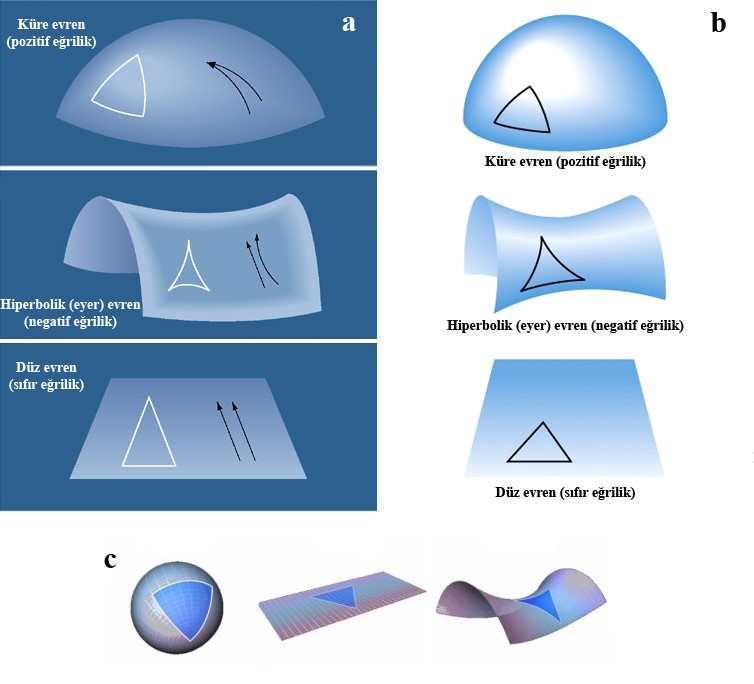
(Küre geometri, eyer geometri, düz geometri.) Bu gösterimler 2 boyutludur.
a, b ve c’yi Türkçeye çevirip düzenleyerek görselleri birleştiren: Alper Çadıroğlu.
(a) University of Oregon, <https://pages.uoregon.edu/imamura/123/lecture-5/topology_universe.jpg>, Erişim: 6 Ağustos 2022 [(+) eklediğim kalıcı arşiv kaydı: https://web.archive.org/web/20221208161434/https://pages.uoregon.edu/imamura/123/lecture-5/topology_universe.jpg]. (b) University of Alberta, <https://sites.ualberta.ca/~pogosyan/teaching/ASTRO_122/lect30a/lecture30a.html>, Erişim: 6 Ağustos 2022 [(+) eklediğim kalıcı arşiv kaydı: https://web.archive.org/web/20221215235725/https://sites.ualberta.ca/~pogosyan/teaching/ASTRO_122/lect30a/lecture30a.html].
(c) University of Groningen, [PDF] <https://www.astro.rug.nl/~weygaert/tim1publication/cosmo2019/cosmology2019.lect5.curved_universe_observational_cosmology.pdf>, Erişim: 27 Kasım 2022, s. 7 [(+) eklediğim kalıcı arşiv kaydı: https://web.archive.org/web/20221208162032/https://www.astro.rug.nl/~weygaert/tim1publication/cosmo2019/cosmology2019.lect5.curved_universe_observational_cosmology.pdf]. (bk. Figür Kaynakları, Figür 34)
Stuart Levy, Tamara Munzner, Martin Bucher, University of Illinois Urbana-Champaign, <http://virdir.ncsa.uiuc.edu/slevy/sciam/nov15.html>, Erişim: 8 Ağustos 2022 [(+) eklediğim kalıcı arşiv kaydı: https://web.archive.org/web/20221215235903/http://virdir.ncsa.uiuc.edu/slevy/sciam/nov15.html]. (bk. Figür Kaynakları, Figür 35-37)
“Şu anda” evrenimizdeki bütün madde (enerji), uzayın her alanına eşit olarak dağıtılırsa, her metreküpte “∼10-23 gramdan -her metreküpte yaklaşık beş hidrojen atomu[ndan]– [-ki bu “kritik yoğunluk”tur, bundan-] daha fazla madde” varsa “uzay”ın eğriliği pozitif olur, daha azsa negatif olur, tam olarak eşitse eğrilik sıfır olur. Evrenimizde madde yoğunluğu, kritik yoğunluğa yakın olduğu için ya da eşitine yakın olduğu için evrenimiz düz geometriye sahiptir, daha doğrusu düz geometriye yakındır. Yanı sıra Big Bang’e doğru geriye gittiğimizde maddenin (enerjinin) “sıkışmış olduğu uzay daha küçük olacağından evrenin yoğunluğu daha büyük olur”. (Yani şunu söyleyebilirim ki evren, başlarda açmamış bir çiçek gibi küremsiydi, sonra açtı ve düzleşti, sonrasında da çiçek solarak eyerleşecek, sonunda da gittikçe çiçeğin yaprakları döküle döküle, evren gittikçe daha çok genişleye genişleye ortada çiçek de evren de kalmayacak, belki tohumdan başka bir evren doğar kim bilir.)
Gözlemlenebilir evrenimizin şekli düz geometriye yakındır, fakat evrenimizin tamamının şekli bilinmemektedir, küre de, eyer de olabilir ya da başka bir durum. Gözlemlenebilir evrenimiz, evrenimizin tamamına oranla “aşırı” küçüktür. Evrenimizin tamamı sıfır eğrilikten uzak olarak örneğin küreyse eğer, 30 cm çapındaki bir balona 10 cm’lik bir doğru çizmeye çalışsak bu, eğri görünür, fakat Dünya çapındaki bir balona 10 cm’lik bir doğru çizsek bu, neredeyse düzdür, bunu eyere ya da başka bir duruma yapsak da sonuç aynıdır, bu, Dünya üzerinde yürüyen bir insanın Dünya’yı düz algılamasına benzer. Gözlemlenebilir evrenimiz, evrenimizin tamamına oranla okyanusta bir damladır. Bunun nedeni evrenin ilk an(lar)ındaki “Şişme”nin devasa olmasıdır.
Evrenimizin ilk anı ya da anlarındaki -ışık hızından hızlı olan- Şişme aşamasında fizik kuralları geçerli olmadığından, kuantum geçerli olduğundan bu anlardaki evrenin şekli hakkında bir şey söyleyemeyiz, daha doğrusu burada evrenin bir şekli yoktur, yani burada şekil sözü geçersizdir.
Gözlemlenebilir evrenimizin kritik yoğunluğa yakın (eşitimsi) olmasını sağlayan madde (enerji) miktarının ∼%5’i normal madde, ∼%25’i karanlık madde ve ∼%70’i ise karanlık enerjidir. Zaten bu durumun da böyle olması gerekir ki çünkü bunların hepsi birer enerjidir. Yani burada denilmek istenen şudur: Kritik yoğunluk belirlenirken-ölçülürken sadece normal madde kullanılamaz, doğal olarak karanlık madde ve karanlık enerji de kullanılır. Yani her metreküpte ∼10-23 grama denk bir enerji ya da yaklaşık 5 hidrojen atomu enerjisine denk bir enerji, yani her metreküpte enerji, bu enerjiden fazla ise evren küre, azsa eyer, eşitse düz olur.
Bir uzay yapısı var da kütle çekimi bunu büküyor değil, evrenin derinlerine indiğimizde kuantumla karşılaşırız ki burada makro evrendeki hiçbir durum ya da tanım geçerli değildir. “Sol ve sağ, ileri ve geri, yukarı ve aşağı [yani 3 boyut], (hatta önce ve sonra gibi [yani zaman])” ve mekân ve de sınır, sınırsız (kenar, kenarsız), sonlu, sonsuz, şekil (biçim) vs. geçerli olmayıp anlamını yitirir.
“Bir cisim hareket ettiğinde ya da bir kuvvet etkisini gösterdiğinde uzay ve zamanın eğriliği değişir ve karşılığında uzay-zamanın yapısı cisimlerin hareketini ve kuvvetlerin işleyişini etkiler. Uzay ve zaman evrende olan her şeyden etkilenmekle kalmaz, olan her şeyi etkiler de. Uzay ve zaman kavramları olmadan evrende gerçekleşen olaylardan söz edemeyeceğimiz gibi, genel görelilik içinde de evrenin sınırları dışında kalan bir uzay ve zamandan söz etmek anlamsızdır.”
Küre modelinde kütle çekimi, genişlemeyi durdurur (yani kütle itimine galip gelir) ve evren başladığı noktaya çöker, düz ve eyer modellerinde ise evren sonsuza kadar genişler.[1]
Kaynak(lar)
[1] Brian Greene, “Evrenin Dokusu…”, age., s. 73-75, 84-87, 288, 290-303, 353-368, 382, 522, 556, 615, 616, 621, 622, 635, 637 (“∼10-23 gramdan ‑her…” ve “sıkışmış olduğu uzay…” alıntıları “Evrenin Dokusu”ndandır.); Brian Greene, “Evrenin Zarafeti…”, age., s. 74-88, 155-160, 184, 188, 189, 277-282, 474, 490 (“Sol ve sağ…” alıntısı “Evrenin Zarafeti”ndendir.); Jim Holt, age., s. 168, 169, 193, 199, 221; Bill Bryson, age., s. 15-17, 43, 112; Stephen W. Hawking, Leonard Mlodinow, “Zamanın Daha Kısa Tarihi” [ISBN: 975-293-499-4], Çeviren: Selma Öğünç, Doğan Kitap, 1. Baskı, Ekim 2006, İstanbul, s. 36-44, 55-58, 61, 62, 82, 103-105 (“Bir cisim hareket…” alıntısı Hawking’dendir.); İbrahim Onur Tüfekci, “Değişken Kozmolojik Sabite Sahip Evren Modellerinde Parçacık ve Olay Ufkunun İncelenmesi”, Hacettepe Üniversitesi, Fizik Mühendisliği Ana Bilim Dalı, Yüksek Lisans Tezi, 2020, [PDF] <http://www.openaccess.hacettepe.edu.tr:8080/xmlui/bitstream/handle/11655/22764/10347913yeni.pdf>, Erişim: 8 Ağustos 2022, s. 1-18 [(+) eklediğim kalıcı arşiv kaydı: https://web.archive.org/web/20221217195448/http://www.openaccess.hacettepe.edu.tr:8080/xmlui/bitstream/handle/11655/22764/10347913yeni.pdf]; Amit Goswami, Richard E. Reed, Maggie Goswami, “Kendini Bilen Evren“, Çeviren: Yasemin Tokatlı, Ruh ve Madde Yayıncılık, 2003, İstanbul, s. 206, 207. Ayrıca bakınız: Dmitri Pogosian, “Lecture 30: The Expanding Universe”, University of Alberta, 7 Nisan 2010, <https://sites.ualberta.ca/~pogosyan/teaching/ASTRO_122/lect30a/lecture30a.html>, Erişim: 6 Ağustos 2022 [kalıcı arşiv kaydı: https://web.archive.org/web/20221215235725/https://sites.ualberta.ca/~pogosyan/teaching/ASTRO_122/lect30a/lecture30a.html]; James N. Imamura, “World Views of the Universe: Reading: Chapter 26, Cosmology”, University of Oregon, 13 Nisan 2017, <https://pages.uoregon.edu/imamura/123/lecture-5/lecture-5.html>, Erişim: 6 Ağustos 2022 [(+) eklediğim kalıcı arşiv kaydı: https://web.archive.org/web/20221217195623/https://pages.uoregon.edu/imamura/123/lecture-5/lecture-5.html]; NASA: WMAP Science Team (yy.), “Will the Universe expand forever?”, NASA/WMAP, 24 Ocak 2014, <https://wmap.gsfc.nasa.gov/universe/uni_shape.html>, Erişim: 7 Ağustos 2022 [kalıcı arşiv kaydı: https://web.archive.org/web/20220529074323/https://wmap.gsfc.nasa.gov/universe/uni_shape.html]; Zeki Kasap, “Weyl Manifoldları Üzerinde Euler-Lagrange ve Hamilton Hareket Denklemlerinin Analizi”, Çanakkale Onsekiz Mart Üniversitesi, Matematik Ana Bilim Dalı, Doktora Tezi, 5 Haziran 2014, [PDF] <http://acikerisim.comu.edu.tr/xmlui/bitstream/handle/20.500.12428/1992/Zeki_Kasap_Doktoratezi.pdf>, Erişim: 8 Ağustos 2022, s. 1-3, 7, 44, 115 [(+) eklediğim kalıcı arşiv kaydı: https://web.archive.org/web/20221217195843/http://acikerisim.comu.edu.tr/xmlui/bitstream/handle/20.500.12428/1992/Zeki_Kasap_Doktoratezi.pdf].